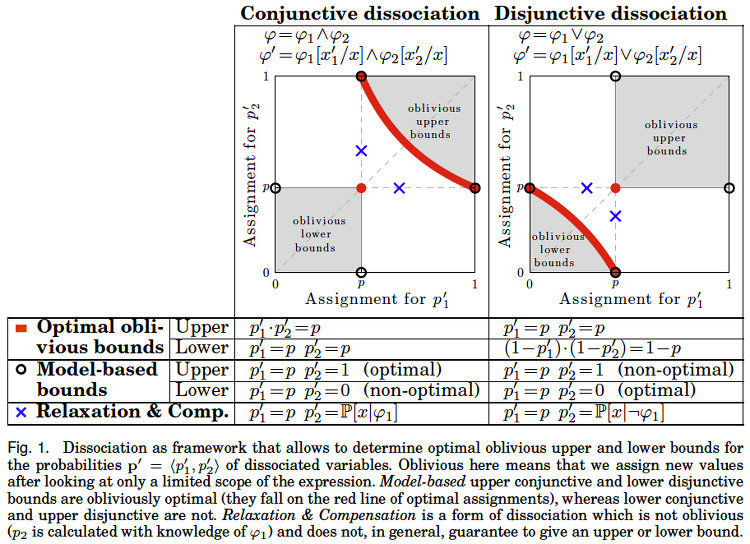
We develop upper and lower bounds for the probability of Boolean functions by treating multiple occurrences of variables as independent and assigning them new individual probabilities. We call this approach dissociation and give an exact characterization of optimal oblivious bounds, i.e. when the new probabilities are chosen independent of the probabilities of all other variables. Our motivation comes from the weighted model counting problem (or, equivalently, the problem of computing the probability of a Boolean function), which is #P-hard in general. By performing several dissociations, one can transform a Boolean formula whose probability is difficult to compute, into one whose probability is easy to compute, and which is guaranteed to provide an upper or lower bound on the probability of the original formula by choosing appropriate probabilities for the dissociated variables. Our new bounds shed light on the connection between previous relaxation-based and model-based approximations and unify them as concrete choices in a larger design space.
We also show how our theory allows a standard relational database management system (DBMS) to both upper and lower bound hard probabilistic queries in guaranteed polynomial time. We call this approach query dissociation and change from the commonly-used possible-world semantics to a new semantics that we call propagation. Conceptually, a dissociated query is obtained from an unsafe query by adding extraneous variables to some atoms until the query becomes safe. We show that the scores for chain queries before and after dissociation correspond to two well-known scoring functions on graphs, namely network reliability (which is #P-hard), and propagation (which is related to PageRank and in PTIME). We then define a unique propagation score for an answer to a self-join-free conjunctive query and prove that it is always an upper bound to the score given by the possible world semantics. We further show that the propagation score can always be evaluated with an instance-independent query plan, that the propagation score is identical to the possible world semantics for all safe queries, and that the concept of propagation is a natural generalization of plans for safe queries to plans for unsafe queries.

Publications
-
Dissociation-based Oblivious Bounds for Weighted Model Counting
Li Chou, Wolfgang Gatterbauer, Vibhav Gogate
UAI, pp. 866-875, 2018.
[AUAI], [preprint], [gs], [bib]
Generalizes the oblivious bounds from TODS 2014 from monotone to non-monotone Boolean functions.
-
Dissociation and propagation for approximate lifted inference with standard relational database management systems
Wolfgang Gatterbauer, Dan Suciu
VLDBJ 26(5): pp. 5-30, 2017. (Special issue on best papers of VLDB 2015, announcement)
[Springer paper], [ACM paper], [arXiv:1310.6257 (full 33 page version, June 2016)], [slides (Uncertainty in Computation workshop, Oct 2016)], [gs], [bib]
Extends VLDB 2015 with all proofs and shows how our approach generalizes the idea of propagation algorithms from graphs to propagation on hypergraphs. We also note that the techniques developed in this paper apply immediately to lifted inference from statistical relational models since lifted inference corresponds to PTIME plans in probabilistic databases.
-
Approximate lifted inference with probabilistic databases
Wolfgang Gatterbauer, Dan Suciu
PVLDB 8(5):629-640, 2015.
[VLDB paper], [ACM paper], [arXiv:1412.1069], [gs], [bib]
Invited to the Special Issue of VLDB Journal on VLDB 2015.
This paper proposes a new approach for approximate evaluation of #P-hard queries with probabilistic databases. In our approach, every query is evaluated entirely in the database engine by evaluating a fixed number of query plans, each providing an upper bound on the true probability, then taking their minimum. Importantly, this algorithm is a strict generalization of all known results of PTIME self-join-free conjunctive queries: A query is safe if and only if our algorithm returns one single plan. We give a detailed experimental evaluation of our approach and, in the process, provide a new way of thinking about the value of probabilistic methods over non-probabilistic methods for ranking query answers.
-
Oblivious bounds on the probability of Boolean functions
Wolfgang Gatterbauer, Dan Suciu
ACM TODS, vol. 39, no. 1, pp. 191-208, 2014.
[ACM paper], [preprint], [arXiv:1409.6052], [Video: dissociation improving mini-bucket (21min)], [SQL code], [gs], [bib]
Prior superseded working paper "Optimal Upper and Lower Bounds for Boolean Expressions by Dissociation": arXiv:1105.2813
This paper develops upper and lower bounds for the probability of Boolean functions by treating multiple occurrences of variables as independent and assigning them new individual probabilities. We call this approach dissociation and give an exact characterization of optimal oblivious bounds, i.e. when the new probabilities are chosen independent of the probabilities of all other variables. By performing several dissociations, one can transform a Boolean formula whose probability is difficult to compute, into one whose probability is easy to compute, and which is guaranteed to provide an upper or lower bound on the probability of the original formula by choosing appropriate probabilities for the dissociated variables. Our new bounds shed light on the connection between previous relaxation-based and model-based approximations and unify them as concrete choices in a larger design space. We also show how our theory allows a standard relational database management system (DBMS) to both upper and lower bound hard probabilistic queries in guaranteed polynomial time.
Funding
This project has been generously supported by the NSF via grants IIS-0915054 (the BeliefDB project) and IIS-1762268. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
